Suppression des arcs
dans les polylignes 2D
Par définition les arcs ou plutôt les segments courbes n'existent que dans les entités "Polyligne2D", ou parle de bulge pour les définir et j'en ai parlé à différents endroits sur ce site et c'est bien des polylignes 2D dont il va être question.
Il peut arriver lors du traitement des dessins qu'il faille supprimer les parties courbes (bulge) dans une polyligne 2D sans toutefois trop nuire à la géométrie avec arcs que ce soit pour travailler ultérieurement en 3D (pas d'arcs ni de courbes) ou pour envoyer vers des machines numériques de découpe ou pour impression 3D.
Je suis parti sur le même principe que pour la segmentation des entités ARC avec les trois méthodes au choix :
- Valeur de FLÈCHE
- Valeur de CORDE
- Valeur de DÉVIATION ANGULAIRE
Une visite de cette PAGE si ce n'est déjà fait vous rafraichira la mémoire.
Voici que on va obtenir par cette routine :
Tant que le programme travaille avec des éléments droits il va simplement mémoriser les coordonnées des sommets de début et fin.
S'il y a plusieurs arcs (bulge) le long de la polyligne et suivant la solution choisie, flèche, corde ou déviation angulaire le programme va calculer à chaque fois qu'une courbe se présente le nombre optimal à utiliser pour résliser une segmentation en éléments de longueur égale.
Autrement dit la polyligne restituée n'aura pas forcément le même nombre de segments pour segmenter les parties courbes.
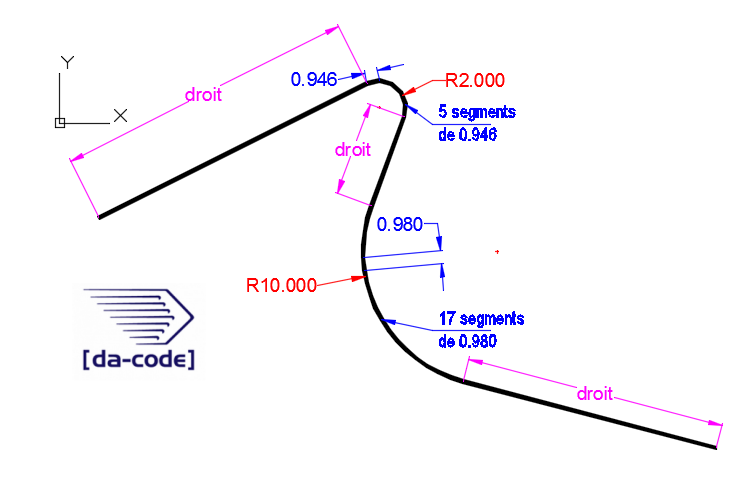
Exemple avec la solution CORDE et une valeur maximale demandée de 1.00 :
On constate un bon fonctionnement car l'arc (polyligne) de 2.00 de rayon est divisé en 5 segments égaux de 0.96 et celui de 10.00 de rayon se retrouve distribué en 17 segments égaux de 0.98.
Ce qui va sans dire va mieux en le disant en constatant que les segments droits ne sont absolument pas modifiés par le programme.
La longueur maximale de la corde (ou de la flèche) n'est jamais dépassée (maximale) et est modulée suivant le rayon du raccord circulaire pour réaliser une division par un entier.
Il n'est pas question de faire 16 cordes de 1.00 et une dernière toute petite avec le reste.
Avant de passer au clavier pour taper ce code je vais expliciter ma façon de faire..
Dans un premier temps :
Sélection de la polyligne
Tout de suite on vérifie que c'en est bien une.
S'il est avéré que l'entité sélectionnée est une polyligne 2D on va tester si elle comporte des segments courbes (bulges), on est d'accord que ce serait inutile de redessiner une polyligne identique à l'origine en l'absence d'arcs et si on n'en trouve pas (bulge).
Un message par l'intermédiaire de la case (alert) et le programme s'arrête (quit) mais non sans prévenir avec une petite pincée d'humour l'utilisateur d'avoir demandé de supprimer des arcs inexistants.
Pour vérifier si elle comporte des segments courbes c'est dans la fonction "liste1042ent" que ça se passe.
J'ai nommé cette fonction ainsi car la liste va extraire les codes DXF 10 (coordonnées) et les codes DXF 42 (valeur de bulge).
Dès qu'une valeur de bulge est différente de 0 (zéro) la variable "arc" passe à T ce qui signifie qu'on a trouvé un segment courbe dans la poyligne sélectionnée par l'utilisateur et que le programme peut continuer.
Si on ne trouve pas de valeur de bulge différente de 0 (zéro) la variable "arc" reste à nil et on lance la case d'alerte citée plus haut avant que le programme s'arrête.
La fonction da:RCL-Bulge calcule le rayon, le centre et la longueur de chaque partie courbe.
Les arguments sont : point de départ (list), point final (list) et valeur de bulge (real).
Elle renvoie une liste contenant les trois calculs.
La proposition des solutions pour segmenter la polyligne à savoir Flèche, Corde ou Déviation angulaire ne se fait pas en affichant une case en DCL (comme pour les arcs) mais en ligne de commande.
Tout ceci est modifiable à l'envi mais je reste dans un but didactique alors je montre plusieurs façons de procéder.
Ensuite grâce au code 90 je vais lancer une boucle qui va traiter chaque élément de la liste "liste1042", soit il y à 0 (zéro) en valeur de bulge (c'est donc un alignement droit) et elle mémorise les coordonnées des sommets soit il a autre chose que 0 (zéro) c'est donc un arc et je lance la fonction tempoarc qui va calculer les sommets à relier pour segmenter la partie courbe.
Arrivé à la fin de "liste1042", les sommets se sont concaténés tout au long du programme dans une liste "listsompol" et il ne reste qu'à lancer le dessin de la polyligne2D résultante.
J'ai mis des commentaires dans le fichier lsp mais je reste joignable par le formulaire de contact pour explication complémentaire ou correction de quelque chose mal expliqué voire d'une faute de frappe.
Voici le fichier LSP :
;;arc-segment-polyligne.lsp (defun tempoarc (ent longarcfleche div sommet) ;mémorisation du PM sur la polyligne "ent" du début de l'arc à diviser (setq pm (vlax-curve-getdistatparam ent (vlax-curve-getparamatpoint ent sommet))) (setq listsom nil) ;mémorisation de la longueur de l'arc (setq longarcfleche1 longarcfleche) ;addition pour avoir le futur PM du point à calculer sur l'arc (setq longarcfleche2 (+ pm longarcfleche1)) ;création de la liste des sommet sur l'arc à diviser (repeat (- div 1) (setq listsom (cons (vlax-curve-getpointatdist ent longarcfleche2) listsom )) (setq n (1+ n)) ;incrémentation pour prochain point sur l'arc (setq longarcfleche2 (+ longarcfleche2 longarcfleche1))) listsom ) ; fin du defun tempoarc ;----------------------------------------------------- (defun liste1042ent (ent / ent-dxf liste1042 arc) ;| fabrique une liste de la forme point bulge point ((-65.0882 -21.7153 0.0) 0.0 (25.6922 22.6121 0.0) -0.254378 (41.4456 21.9193 0.0) 0.0 (122.991 -27.1991 0.0) 0.0) qui est la liste des sommets de la polyligne avec un 0.00 si c'est un segment droit et la valeur de bulge si c'est un arc je rajoute la variable elev pour avoir un triplet de valeur x y et z |; (setq ent-dxf (entget ent) elev (cdr (assoc 38 ent-dxf)) n 0 ) ;| extraction de la valeur d'élévation de la polyligne dans la variable "elev" pour renseigner le Z dans la liste des points de la future polylihne de discrétisation |; (repeat (length ent-dxf) (cond ((= 10 (car (nth n ent-dxf))) ;si c'est un sommet, enregistrement des coordonnées (setq liste1042 (cons (list (car (cdr (nth n ent-dxf))) (cadr (cdr (nth n ent-dxf))) elev ) liste1042 ) ) ) ((= 42 (car (nth n ent-dxf))) ;| si c'est un bulge, enregistrement de la valeur 0.00 le cas échéant si pas d'arc |; (setq liste1042 (cons (cdr (nth n ent-dxf)) liste1042)) (if (/= 0.0 (cdr (nth n ent-dxf))) (setq arc T) ) ) ) (setq n (+ 1 n)) ) (if arc liste1042 (progn (alert "Saperlipopette !!! \n\nIl n'y a pas de segment courbe \nle programme de segmentation ne fera donc rien..." ) (quit) ) ) ) ;fin de liste1042ent ;| traitement des bulge dans des polylignes fonction qui renvoie une liste du rayon du centre et lonqueur de l'arc trois arguments : p1 point de départ de l'arc (bulge) triplet x y z p2 point final de l'arc (bulge) triplet x y z b valeur du bulge (code 42 de la polyligne) nombre réel (avec signe) |; (defun da:RCL-Bulge (p1 p2 b / c r l) ;p1 début du bulge | p2 fin du bulge | b valeur du bulge (setq r (/ (* (distance p1 p2) (1+ (* b b))) 4 b) ;rayon du bulge c (polar p1 (+ (angle p1 p2) (- (/ pi 2) (* 2 (atan b)))) r) ;centre du bulge l (abs (* (/ (* r (* pi 2)) (* pi 2)) (* 4 (atan b)))) ;longueur de l'arc bulge ) (list (abs r) c l) ;renvoie la liste du rayon, du centre, longueur de l'arc ) ; fin de da:RCL-Bulge ;----------------------------------------------------------- (defun c:Seg-Pol (/ listsom ListeSomPol) (setq ent (car (entsel "\nChoix de la polyligne\n"))) (if (= "LWPOLYLINE" (cdr (assoc 0 (entget ent)))) (progn (setq liste1042 nil) (setq liste1042 (reverse (liste1042ent ent))) ) (progn (alert "\nNe fonctionne qu'avec une POLYLIGNE") (quit) ) ) (setq rep (strcase (getstring "\nFleche ou Corde ou Déviation\n") ) ) (cond ((= rep "F") (setq valeur (getdist "\nValeur de la FLÈCHE maximum : \n")) ) ((= rep "C") (setq valeur (getdist "\nValeur de la CORDE maximum : \n")) ) ((= rep "D") (setq valeur (getdist "\nValeur de la DÉVIATION maximum : \n") ) ) ) ;_ Fin de if (setq i 1) ;assoc 90 est le nombre de sommets la boucle se fait nombre de sommets moins 1 (repeat (- (cdr (assoc 90 (entget ent))) 1) (if (= 0.0 (nth i liste1042)) (setq ListeSomPol (append (list (nth (+ i 1) liste1042) (nth (- i 1) liste1042) ) ListeSomPol ) ) ) ;fin if c'est un segment droit (if (/= 0.0 (nth i liste1042)) (progn (setq lst-rcl (da:RCL-Bulge (nth (- i 1) liste1042) (nth (+ i 1) liste1042) (nth i liste1042) ) ) (setq cordebrut (sqrt (- (* 8.0 (* (car lst-rcl) valeur)) (* 4.0 (* valeur valeur))))) (setq div (+ (fix (/ (last lst-rcl) cordebrut)) 1)) (if (= rep "F") ;option FLECHE (progn (setq cordebrut (sqrt (- (* 8.0 (* (car lst-rcl) valeur)) (* 4.0 (* valeur valeur))))) (setq div (+ (fix (/ (last lst-rcl) cordebrut)) 1)) (setq longarcfleche (/ (last lst-rcl) div)) (tempoarc ent longarcfleche div (nth (- i 1) liste1042) ) (setq ListeSomPol (append listsom ListeSomPol)) ) ) (if (= rep "C") ;option CORDE (progn (setq div (+ (fix (/ (last lst-rcl) valeur)) 1)) (setq longarcfleche (/ (last lst-rcl) div)) (tempoarc ent longarcfleche div (nth (- i 1) liste1042) ) (setq ListeSomPol (append listsom ListeSomPol)) ) ) (if (= rep "D") ;option DEVIATION (progn (setq devia (* (/ valeur 200.0) pi) ;(atof valeur) ang (abs (* 4.0 (atan (nth i liste1042)))) long (last lst-rcl) div (+ (fix (/ ang devia)) 1) longarcfleche (/ (last lst-rcl) div) ) ;_ Fin de setq (tempoarc ent longarcfleche div (nth (- i 1) liste1042)) (setq ListeSomPol (append listsom ListeSomPol)) ) ) ) ) ;fin if c'est un bulge (setq i (+ i 2)) ) ;fin du repeat ;lancement du dessin de la polyligne avec les points de ListeSomPol (entmake (append (list '(0 . "LWPOLYLINE") '(100 . "AcDbEntity") '(100 . "AcDbPolyline") (cons 90 (length ListeSomPol)) '(70 . 0) ;1 pour fermée, 0 pour ouverte ) ;_ Fin de list (mapcar '(lambda (p) (cons 10 p)) ListeSomPol) ) ;_ Fin de append ) (princ) )